 [Physics 4] Speed, Velocity And Acceleration (Solutions)1. A baseball is pitched at 40 m/s (90 mph) in a Major League game. The batter hits the ball on a line drive straight toward the pitcher at 50 m/s (112 mph). Determine the the acceleration of the ball if it was in contact with the bat for 1/30s solution
[Physics 4] Speed, Velocity And Acceleration (Solutions)1. A baseball is pitched at 40 m/s (90 mph) in a Major League game. The batter hits the ball on a line drive straight toward the pitcher at 50 m/s (112 mph). Determine the the acceleration of the ball if it was in contact with the bat for 1/30s solution Acceleration is the rate of change of velocity with time. Since velocity is a vector, this definition means acceleration is also a vector. When it comes to vectors, direction matters as much as size. In a simple one-dimensional problem like this one, directions are indicated by algebraic sign. Every quantity that points away from the batter will be positive. Every quantity that points toward him will be negative. Thus, the ball comes in at −40 m/s and goes out at +50 m/s. If we didn't pay attention to this detail, we wouldn't get the right answer.
v0 = −40 m/s
v = +50 m/s
Δt = 1/30s
a = ?
a = v−v0/Δt = (+50 m/s) − (−40 m/s) / 1/30s
a = (+90 m/s)(30s
−1) = +2700 m/s
2 a = 2700 m/s
22. The diagram above represent the velocity time graph of a body in motion. The total distance traveled by the body is 195m. Calculate the acceleration of the body in section OP of the graph Solution U = O, S = 195m, t = 6sec
V = U + at
V = o + a6 = 6a m/s
Distance traveled;
S = (1/2 x 6 x V) + (5 x V) + 1/2 x 10 x V
S = 3V + 5V + 5V
S = 13V
Therefore;
195 = 13V
AND Recall; V = 6a m/s
13V = 13 x 6a
= 78a
a = 195/78
a = 2.5m/s
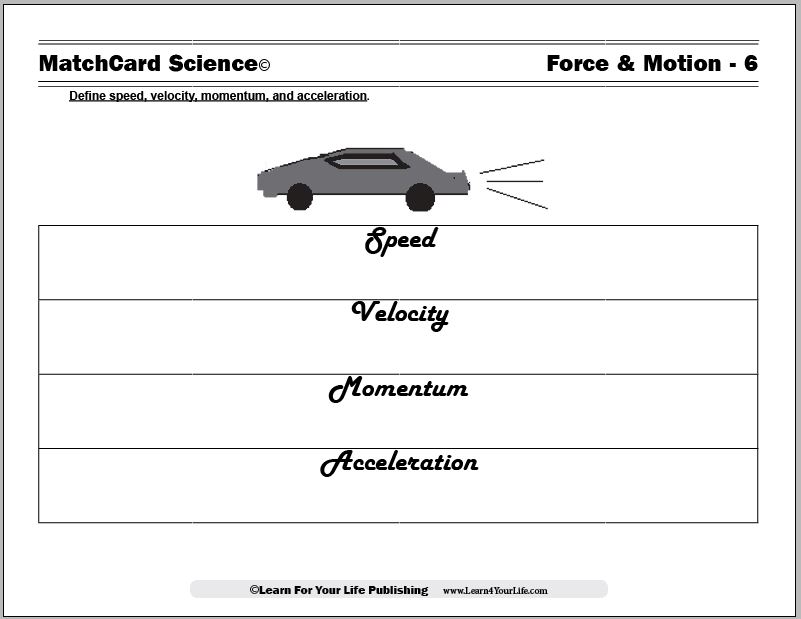
23. A particle is dropped from a vertical height h and falls freely for a time t. With the aid of this sketch, h varies with 
A. i and t
B. t and t
2 ✔
C. h and t
D. h and t
24. A particle is projected horizontally at 15ms-1 from a height of 20m.
Calculate the horizontal distance covered by the particle just before hitting the ground. [g = 10 ms-2]Solutions Let R represent the horizontal distance covered at time, t.
h = ½gt2
20 = ½ x 10 x t2
t = 2s
R = ut
= 15 x 2 = 30m
4. A body at rest is given an initial uniform acceleration of 6.0 ms-2 for 20s after which the acceleration is reduced to 4.0 ms-2 for the next 10s. The body maintains the speed attained for 30s.
from the velocity-time graph of the motion given, calculate the average speed during the same time interval. 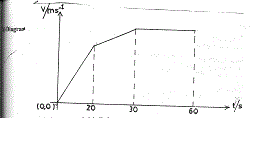 Solutions
Solutions Let V1 = maximum velocity after 20 sec.
V2 = maximum velocity after 30 sec.
(I)
Then V1 = 6x20
V1 = 120 ms-1
Also V2 – V1 = 4x10
V2 – V1 = 40
V2 = 120 + 40
V2 = 160 ms-1
Maximum speed = V2 = 160ms-1
(II)
Total distance covered = Area of Δ + Area of trapezium after 1st 30 seconds
= ( ½ x 20 x 120) + ½ (120 + 160) x 10
= 1200 + 1400
= 2600m
(III)
Average speed = Total distance / Total time
= 2600/30
= 86.67 ms-1
5. For the velocity time graph shown in the figure, the distance covered by the body in the last two seconds of its motion is what fraction of the total distance travelled by it in all the seven seconds? Solutions
Solutions Distance covered is equal to the area under velocity-time graph.
Distance in last two seconds s2 = 1/2 × 8 × 2 = 8m
Total distance = 1/2 × 8 × (6+2) = 32m
Fraction of the distance covered by the body in the last two seconds of its motion to total distance traveled by it in all the seven seconds is 8/32 = 1:4 or 1/4
6. A ticker-timer uses 1/5s to 8cm length of a ten tick. What is the velocity? Solutions Velocity = Displacement/time
= 8 ÷ 1/5
= 40cm/s
7. The SI unit of speed and velocity isA. m/s ✔
B. m/s2
C. m
D. s/t
8. Speed can be define as ______A. the rate of change of time only
B. the rate of change of distance with time ✔
C. the rate of change of distance only
D. the rate of change of velocity with time
9. Acceleration can be define as ________
A. the rate of change of velocity with time ✔
B. the rate of change of distance with time
C. the rate of change of time alone
D. Non of the above
10. The SI unit of acceleration isA. m/s
B. m/s2 ✔
C. m
D. s/t